Quick step-by-step tutorial

First of all, if you have not installed IGNNITION yet, please go to the installation guide to quickly install it with PyPI.

In this tutorial, we will learn how to solve the shortest path using a Message Passing Neural Network (MPNN). For sake of simplicity, we will present a very simple architecture, which of course could be improved. Before starting, if you are not familiar with this type of NN, we strongly recommend first reading the section What is a GNN where we explain in detail the different phases that an MPNN has. To do so, we are going to cover four main steps:

Understanding the problem
Building the Dataset
Designing and implementing the GNN
Training and evaluation
Debugging

Understanding the problem 

In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. As an example, in the following graph, the shortest path between N1 and N3 is N1, N5, N3.

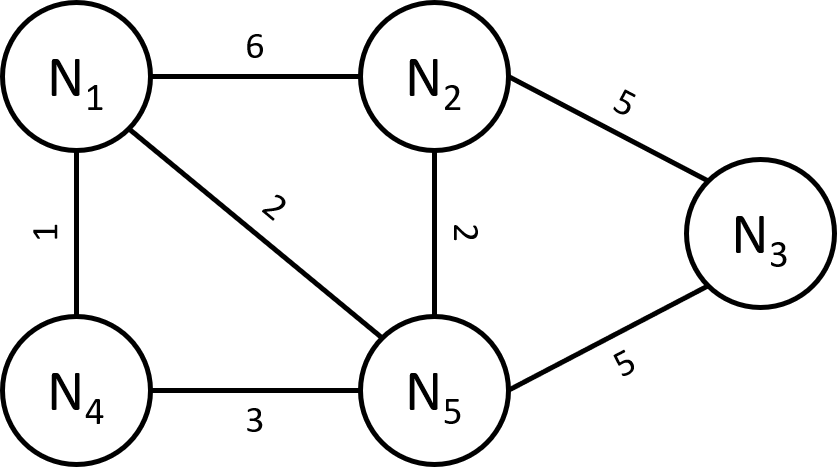
Since shortest paths can be understood as sequences of nodes, and therefore, sequences can have different lengths we are going to transform this problem into a binary classification one. In this case, we are going to classify the nodes depending on whether a node is in the shortest path or not. Following the example stated before, the nodes should be classified as:

N1	N2	N3	N4	N5
1	0	1	0	1

Building the Dataset 

The IGNNITION framework input pipeline requires the dataset to be in a JSON format. In this regard, IGNNITION accepts datasets formed by JSON files –potentially many of them– as well as tar.gz compressed files, each of which contains one single JSON file.

For this tutorial, we are going to build a simple dataset that includes one type of node, one node feature, and one edge feature. However, the framework accepts any amount of features and node types. You can check how to build the dataset in the section Dataset.

In this particular case, the nodes are going to be encoded using a a binary feature called “src_tgt” that tells us whether a node is the source or the destination of the shortest path is calculated. For the example graph we provided before, the different nodes will be encoded as:

N1	N2	N3	N4	N5
1	0	1	0	0

We provide a pre-generated dataset here. This dataset contains 10000 graphs with a number of nodes between 5 and 15 and weights that go between 1 and 10. Also, the probability that an edge exists between two pairs of nodes is set to 30%.

In order to simplify the problem, all the Shortest Paths included in the dataset are unique. This means that between two pairs of nodes only exists one shortest path. Also, all the shortest paths are symmetric. This means that the shortest path between any pair of nodes v1 and 2 is the same as v2 and 1 in reverse order. Finally, it is possible that the different graphs are not connected. However, all the nodes in the graph will always be connected to one or more nodes. This means that there will never exist one node in the graph that has degree 0.

If you want to create a new dataset for this specific tutorial, we provide a Python script called data_generator.py where you can modify all the aforementioned parameters.

In this script, you will notice that for each of the samples forming the dataset we generate a NetworkX graph. In this graph, we initialize each of the vertices as well as the edges connecting them. Then, we create the node features which in this case would simply be src-tgt, indicating whether a node is a source or the destination of the shortest path we are looking for. Additionally, each node has an attribute entity indicating its entity name (for this example, all the vertices of the graph are of type node), and the node’s label. Finally, we create a parameter weight for each edge of the graph which defines the distance for every two connected nodes. Note that these will be the distances that we will try to minimize.

Designing and implementing the GNN 

In order to design the GNN model based on a Message-Passing structure, we need to basically focus on four main steps:

1. Hidden state initialization
2. MPNN architecture

To do so, we will need to create a model_description.yaml which will contain all the information regarding our model architecture. Note that you can find the final implementation in model_description.yaml.

1. Hidden state initialization 

To encode the information of the different nodes found in the graph, MPNN uses a vector of a predefined size that is called state (sometimes also the hidden state). In this problem, the different nodes’ states are initialized with the feature “src_tgt”. To do so, we are going to generate an entity that will be called node with a state dimension of 16. To define the initialization of the state, we use the build_state operation which will place feature “src_tgt” at position 1 and will add 0s at the rest of the 15 position. To do so, we need to add to the model description the following lines:

entities:
- name: node
  state_dimension: 16
  initial_state:
    - type: build_state
      input: [$src_tgt]

In this case, we only have one feature per node. Note however that the field input potentially accepts a list of any variable defined in the JSON dataset. Moreover, notice that all the features that reference information of the dataset are preceded by a $ symbol, so as to indicate that this keyword represents a feature.

An important aspect to consider to design a GNN is the state dimension, which can be understood as a hyperparameter that needs to be tuned. Since the problem we are facing is a simple one, a state size of 16 is more than enough.

For a more detailed explanation on how to build the entities object and what parameters accept or not, we suggest on reading the section Entity definition.

2. MPNN architecture 

At this point, we must define the core part of the MPNN algorithm, which is the neural message-passing phase. In this phase, different messages are sent between nodes that are used to update the hidden state of each node. These hidden states will be finally used as input to the readout phase to generate the final input.

Message phase 

Defining the message phase is probably the one that has the most impact on the model. In this case, we are going to define a single message-passing phase. This means that we are only going to have one stage where the different nodes exchange messages between them. To do so, we need to add the following information to the model definition:

message_passing:
  num_iterations: 4
  stages:
    - stage_message_passings:
      - destination_entity: node
        source_entities:
          - name: node

First of all, we are defining the number of message-passing iterations. Secondly, we need to define the destination and the source entity. In this case, since we only have one entity the source and the destination are the same. Observe that we do not define explicitly the connections between the nodes, as they will all be found in the dataset, and IGNNITION will simply adapt to them.

With the previous lines of code we defined which entities exchange messages and how many times. However, the message has not yet been defined. For this particular example, we are going to define the message function using a Feed Forward Neural Network which, for each of the edges between two nodes will take as input the hidden state of the source node and the weight encoded as a feature of the edge. To do so, firstly, we need to define the architecture of the FFNN. The model_definition.yaml contains a specific object to define all the NN that are used in the different stages of the GNN. In this case, the NN used for the message creation (that we are going to refer to it as message_function) will have two fully connected layers with 32 and 16 units respectively for each layer and with a ReLU activation.

neural_networks:
- nn_name: message_function
  nn_architecture:
  - type_layer: Dense
    units: 32
    activation: relu
  - type_layer: Dense
    units: 16
    activation: relu

Note that the IGNNITION framework accepts a pipeline of different operations in all of the different message-passing stages. The last operation of each one (in this case the first and the last are the same since we only have one) needs to have the proper output shape. That is the reason why the last layer of the message function has 16 output units, to have the same shape as the destination hidden state.

Now we have defined the way the message needs to be created, we need to specify it to the model. To do so, we need to append to the stage message passing the following lines:

message_passing:
  num_iterations: 4
  stages:
    - stage_message_passings:
      - destination_entity: node
        source_entities:
          - name: node
          message:
            - type: neural_network
              nn_name: message_function
              input: [source, $weights]

These lines simply tell the model that the operation used to create the model is a NN that is identified with the name message_function and takes as input the source hidden state of the model and the weights that we defined for each of the edges in the dataset. Again, we write $weights to indicate that this is a feature that can be found in the dataset.

Again, we refer the user to keywords, where we provide full detail of each of the available keywords.

Update phase 

Once all the messages are sent, the different nodes need to collect all the messages that they received and use a function to aggregate them and transform them into something that the update function is able to understand. In this case, and for the sake of simplicity, we are going to use a min aggregator that will simply use the minimum among all the messages to use as input of the update function. To define the aggregation function we need to use the following line:

aggregation:
  - type: min

Again, note that more complex aggregation functions can be defined using the framework.

Once we have defined the aggregation function, it is time to define how the hidden state of each node is updated. Usually, the Update function takes as input the hidden state of the node and the output of the aggregation function. In this case, we are going to define as update function a Recurrent Neural Network that takes as initial state the current hidden state of the node and updates it using the output of the aggregation function. As we did in the previous section, we first need to define how the update function is defined using:

- nn_name: update_function
  nn_architecture:
    - type_layer: GRU

Since we are using a neural network as the update function, we need to add it to the neural_networks object and then, refer to it in the message passing definition by adding the following:

update:
  type: neural_network
  nn_name: update_function

Readout phase 

Once the message-passing has ended we need some way to combine the different hidden states to produce the output. This is where the Readout function comes in. In this case, since we want to predict individual features (one for each node). Thus, the readout phase only needs to take as input each of the node’s hidden state and output, for each of them, if the node is in the shortest path. To do so, as we did with the other phases, we need to specify the neural network that will work as the readout function adding it to the neural_network object:

- nn_name: readout_function
  nn_architecture:
  - type_layer: Dense
    units: 16
    activation: relu
  - type_layer: Dense
    units: 8
    activation: relu
  - type_layer: Dense
    units: 1
    activation: sigmoid

In this case, we created an FFNN with 3 layers, the last layer of which has only 1 unit and a sigmoid function as activation. This is because, as stated before, we are trying to predict a single binary variable.

Finally, we only need to create the readout object:

readout:
- type: neural_network
  input: [node]
  nn_name: readout_function
  output_label: [$sp]

In it, we simply need to define the input that will take the readout function, which in this case is simply the name of the entity, the states of which we use as input (i.e. node). Then we reference the NN that works as a readout function by its name and finally, reference the feature from the dataset with which the loss function is going to be computed (in other words, the label we aim to predict). Concretely, in this case, the output_label is a feature that can be found in the dataset named sp. Moreover, as done before, we write $sp to indicate that sp refers to data from the dataset.

Training and evaluation 

In main, we provide the file that we used for the execution of this model.

In it, we simply create the model by indicating the model_path, this being where the file training_options.yaml file is located. In this case, the main.py file is already located there. Then we simply call the train_and_validate() function of the model, which starts the training. For more details regarding how to call the functionalities of our model, check train and evaluate.

After doing so, we obtain a new directory checkpoint in the output_path provided in the training_options.yaml file. There we can see that a new directory has been created for this experiment(indexed by execution date). Inside this directory, we find the directory ckpt with the checkpoints saved every epoch of the training and the directory logs, with the Tensorboard visualizations.

For sake of the explanation, let us visualize the Tensorboard statistics by executing the following command in the scope of the logs directory.

tensorboard --logdir ./

Then, by accessing the following link, we can visualize the collected statistics. Below we provide a table with a brief overview of the most relevant statistics of the validation set found in the Tensorboard visualization.

Accuracy	Precision	Recall	AUC
0.9042	1.0000	0.7592	0.9076

Debugging 

Finally, we show how to debug the model by visualizing the internal architecture of the GNN. To do so, find the directory that the call model.computational_graph() created. This new directory computational_graph is also located in the output_directory, and contains a specific folder inside for the given experiment -indexed by date of execution-.

Place yourself within the scope of our experiment’s directory, and execute the following command:

tensorboard --logdir ./

Then, again, visit link where you will observe the resulting computational graph. If you want more information regarding the interpretation of this graph, please visit debugging assistant.